Beyond Numbers: Navigating the Mathematical Landscape

In the vast realm of mathematics education, the integration of innovative teaching methods plays a pivotal role in fostering comprehension and mastery. This exploration delves into three key aspects: the use of place value words for teaching arithmetic, the visualization of functions through graphs, and the utility of the Chi-Square distribution table in statistical analysis. Each of these components contributes to a holistic approach in enhancing mathematical understanding and problem-solving skills.



Place Value Words in Arithmetic Education:

Understanding the foundational concept of place value is crucial in developing a solid mathematical foundation. Place value words provide a linguistic approach to teach and reinforce this concept. Instead of simply reciting numerical values, students learn to articulate numbers using words, emphasizing the significance of each digit's position in a numerical expression.

By incorporating place value words, educators can guide students in comprehending the hierarchical structure of numbers. For instance, breaking down the number 4,528 into "four thousand, five hundred, twenty-eight" not only reinforces the magnitude of each digit but also promotes fluency in expressing numerical values verbally. This verbal reinforcement bridges the gap between abstract numerical concepts and real-world applications, enhancing students' ability to apply mathematical knowledge in everyday scenarios.

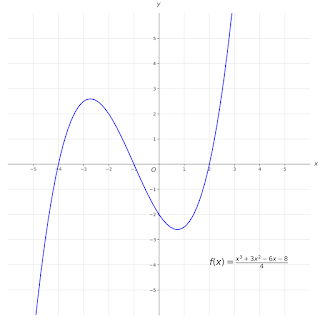
Graphs Representing Functions:

Graphs are powerful tools for visualizing mathematical functions, providing a dynamic representation of relationships between variables. In teaching mathematics, particularly functions, graphing serves as a bridge between abstract equations and tangible visualizations. Whether linear, quadratic, or exponential, graphs that represent functions offering a visual aid that enhances conceptual understanding.

Graphs not only facilitate the interpretation of mathematical relationships but also encourage critical thinking and problem-solving. For example, a linear function's graph appears as a straight line, conveying a constant rate of change. Meanwhile, a quadratic function's parabolic curve illustrates a different kind of mathematical behavior. By exposing students to diverse functions and their graphical representations, educators enable them to grasp the nuances of mathematical concepts in a more intuitive and engaging manner.

Table of Chi-Square Distribution in Statistical Analysis:

The Chi-Square distribution table is a fundamental tool in statistical analysis, particularly in the field of hypothesis testing and goodness-of-fit assessments. Understanding and effectively utilizing this table is essential for students and researchers alike. The table provides critical values for the Chi-Square statistic, allowing users to determine the probability associated with observed data and assess the significance of relationships.

In a Chi-Square distribution table, degrees of freedom and significance levels guide statistical decisions. As students explore statistical analyses, they learn to interpret the table's values, comparing observed and expected frequencies to draw meaningful conclusions. This practical application of statistical theory contributes to a broader understanding of probability and hypothesis testing, preparing students for analytical challenges in various academic and professional domains.

Integration of Concepts for Comprehensive Mathematical Proficiency:

Bringing together place value words  function graphs, and the Chi-Square distribution table creates a comprehensive approach to mathematical education. By intertwining linguistic expression with numerical understanding through place value words, students develop a richer comprehension of arithmetic. Transitioning from numerical equations to visual representations of functions through graphs enhances their ability to conceptualize abstract mathematical relationships.

The inclusion of statistical analysis and the Chi-Square distribution table further extends mathematical proficiency into the realm of data interpretation. Students gain practical skills in hypothesis testing and significance assessment, fostering a well-rounded mathematical skill set that is applicable across disciplines.

Location: North Sydney NSW 2060, Australia

Comments

Post a Comment

Popular posts from this blog

Unlocking the World of Mathematics

Image
Mathematics, often regarded as the language of the universe, encompasses a diverse range of concepts that are fundamental to our understanding of the world. In this exploration, we delve into three crucial aspects of mathematics: place value, function graphs, and table of chi square distribution . Each plays a unique role in mathematical understanding, from foundational principles to statistical analysis. Place Value and its Significance: Understanding place value is the cornerstone of mathematical literacy. It defines the value of each digit in a number based on its position. For instance, in the number 245, the digit '5' represents five units, '4' represents four tens, and '2' represents two hundreds. This system allows us to grasp the magnitude of numbers, facilitating arithmetic operations and providing a framework for more complex mathematical concepts. Place value extends beyond basic arithmetic, playing a crucial role in decimal numbers and scientif
Read more

Unlocking the Secrets of Numbers

Image
Mathematics is a language that enables us to understand and interpret the world around us. In this exploration, we delve into three essential mathematical concepts: place value, graphs representing functions , and the chi-square distribution table. Each of these concepts plays a crucial role in different branches of mathematics, offering insights into the structure and relationships within numerical and statistical realms. Understanding Place Value: Place value is the foundation of our number system, and a solid grasp of this concept is essential for mathematical success. It involves understanding the value of each digit in a number based on its position. For instance, in the number 7,542, the 7 represents thousands, the 5 represents hundreds, the 4 represents tens, and the 2 represents units. One effective way to teach place value word is through interactive and visual methods. Consider using colorful charts or manipulative that allows students to physically move digits around,
Read more

A Comprehensive Guide to Mathematical Understanding

Image
   Teaching Mathematics: A Comprehensive Approach   In the ever-evolving landscape of mathematics education, integrating diverse and effective teaching methods is essential for fostering understanding and enthusiasm among students. This article explores an interdisciplinary approach that combines three vital components: graphs that represent functions , place value words , and a table of Chi-Square distribution . This amalgamation creates a rich learning experience that not only elucidates core mathematical concepts but also highlights their interconnectedness.       1. Graphs Representing Functions     Graphs that represent function . Understanding functions is fundamental to mathematical literacy, and graphs serve as powerful tools in representing these functions visually.   Introduction to Functions:   Begin by demystifying the concept of functions. Define a function as a relationship between input and output values, emphasizing the dynamic nature of this connection.   Coordinate
Read more